Exploring the design space of "remote scene approximation".

A work-in-progress report.

For once, I'll make the intro short. The following will be a quasi-diary of an R&D idea I've been toying with lately. Not quite a diary as - although I do have chronological notes, I will digest them into a more cohesive narrative here.

For me, this is useful as by explaining things, often more is notice, a form of "duck coding" if you wish. For you, I'm not sure but there might be some value in having some insight on the way I think. We (in the industry/research) always publish the end idea - the working innovation, and we know that's leaving a lot of value on the table, but few dedicate time to change this status quo - so I wanted to go back to the OG spirit of blogging, to keep a diary or rather, lab notes.

Problem:

- Approximation: Replace (far) chunks of scene geometry with a cheaper (time and space) representation.
- Remote: Source geometry is not present on client - the approximation is to be dynamically computed on remote machines and transmitted to clients.

Assumptions:

- Transmission costs are very important (over-the-wire size).
- Generation costs are important as well - can't assume that we know when or how the source geometry will change.
- Could use GPUs on the cloud, but it's interesting to explore a CPU solution as well.
- Aim to optimize client-side performance and memory first and foremost, download/startup time second.
- We can design a system to be resilient to certain changes (e.g. objects under rigid transform might be ok in a given system w/o the need to regenerate) - but that would only lower the "rate of surprise" - other things can still change that we would force to regenerate areas of the world (e.g. textures, colors, topology, etc).
- Assume the scene does not have much structure, or rather, the structure does not have a reliable rendering semantic. I.e. triangles are divided among scene parts, but a logical object (e.g. a house, a tree, etc) can be made by many small parts, and vice-versa, a part could represent a large chunk of scene geometry with multiple logical objects (e.g. a city). Ideally, we would work on arbitrary polygon soups.

Initial mapping of the solution space:

- Space: World/object space or view space? In other words, view-independent or not?
- Representation: Images? Points? Meshes? Volumes?
- Delivery: GPU-ready format (low-poly mesh, textures, simple enough shaders) or transcoding/finalization on client?
- Structure: Regular (implicit) or not? For example, a heightfield is a mesh with a regular structure, it requires less data per vertex, but each vertex is less "powerful" being constrained in its position. Also, regular structures are usually much easier to delta-update or hierarchical LOD/stream.
- Compressibility: Related to structure - everything can be compressed (transmitted optimally), with enough effort - but often having more DOFs (e.g. more arbitrary structure) with fewer, more "powerful" elements, might not pay off over the wire if each element is then less compressible...


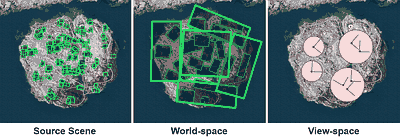
View-independent methods are superior from a generation perspective, as servers don't need to specialize per player/view. Mesh or image-based would be efficiently renderable by clients. Incremental formats might or might not be needed depending on the rate of updates.

Some obvious choices:

- Octahedral impostors
- Billboard clouds also related
- Remeshing-based (retopology) LOD


Octahedral impostors
Various kinds of "billboard" Impostors
Remeshing example
Note that some view-independent methods also have view-dependent subsets, which could be an interesting characteristic. For example, octahedral impostors are view-independent when we bake them over a full sphere of directions, but we can prioritize baking and/or transmission of certain viewpoints first, thus making them more flexible.

If transcoding is allowed, more options could unlock. On client, we could generate and cache transcodes - from whatever fancy format optimized for generation and transmission to, for example, conventional card impostors. This means we could use something that is not directly fast to render in real-time, but cheap to transmit, and then make it real-time by client-side processing.

Lastly, server-side view-dependent methods though are not to be completely disregarded, especially if/as it might be possible to share a view-dependent representation among multiple nearby viewpoints.

If we expand the search with the aforementioned ideas in mind, a few more options come to mind:

- NERFs! Obviously, since their inception, there have been so many papers that I won't even bother linking any. Albeit this specific approach to turning rendering differentiable is certainly a stroke of genius, I don't think it's likely to be optimal as a representation.
- These days you can't say NERF without thinking Gaussian Splatting, another genius idea in its simplicity...
- In general, we can think of volumetric representations, be they for geometry (surface) or lightfields (radiance)...
- ...and every time we think of volumes, we should think of point clouds, which end up being somewhat related [*1].
- When we think about point clouds, we should think about heightfields and depth buffers [*2].


[*1] - Discretize the coordinates of points in a cloud, then compress them by encoding the common binary prefixes between points... and you end up with something very similar to a binary voxel octree!
[*2] - Turns out that if you want to generate a point cloud, a nifty way is through raster, just capture the scene from a set of viewpoints and go from the depth buffer to points in 3d space. Then, if I were to store such a special point cloud, I wouldn't need 3d points, but just the list of depths (one dimension) and the camera parameters!

Observations:

Now, this already is interesting, just starting with trivial ideas one can notice a few things...

First, it seems that one axis of choice will be in the relationship between expressing visibility (shape), versus appearance (color, surface attributes, and so on).
This is a natural and universal thing in 3d modeling. Certain things are modeled as geometry, certain others are left as surface properties.


Evolution of Lara Croft models
We can generally notice a natural evolution, or how this tradeoff shifts based on polygon requirements. Low-poly art tends to "bake" more of the look via textures, while if we go all the way to offline rendering we might not even get textures anymore in the renderer (e.g. Reyes-style micropoligons), surviving only as a tool for ease of authoring (and perhaps antialiasing).

Normally though this choice is in the hands of the artists - hand optimizing to fit in whatever frame budget whatever they imagine is most important, so we don't think about it much. Here as we are thinking broadly about generating a new representation from the source art, the balance is part of our algorithm.

Another way of looking at this is that if we couple some geometric information with some form of baked irradiance, we can reproject the latter and extend its validity to a set of viewpoints - thus visibility "pays itself back" by removing some redundancy in the appearance encoding.

Second thing to highlight is how much there seem to be relations, almost a continuum, between ideas.

For example, to me, if you squint a bit, a billboard cloud seems closely related to octahedral impostors! We are taking appearance information from a set of directions, with the impostors on a regular view sampling so we can do some easy interpolation in a shader, while for billboards we can freely decide the planes of projection because we'll use the raster to render all of them out - at the expense of not being able to be "fancy" as we can't decide per-pixel what to do...

Now we know that for octahedral impostors we can use depth to perform some parallax adjustment between the captured views/slices... well then what if we do the same for something like billboards? We could have depths there create a displacement of the plane, instead of keeping it flat, so that we can conform to the source geometry better...


D(epth)Mesh (top), Geometry Images, and some older tests I did to approximate occluders (bottom left to right)
If we are thinking of generating heightmaps, then we can imagine we need some way to remove "fake walls" - erroneous geometry that gets generated around depth discontinuities of a given point of view. See this recent post on my old blog, for example. This in turn is related to heuristics we use in any screen-space technique (think SSAO etc) to avoid artefacts due to the "blindness" of depthmaps... And from there, we know a possible solution would be depth peeling, and/or using multiple points of view, properly weighted.


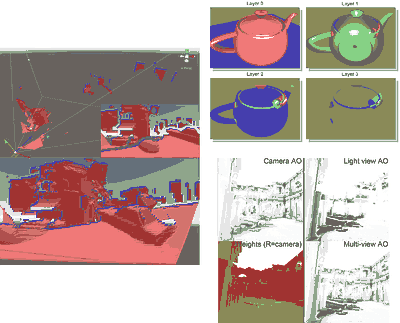More old occlusion tests, removing walls due to depth discontinuities; Depth peeling (top right); Multi-view AO (bottom right)
But now if we think about multiple views and weighting... we connect back to octahedral impostors. These are just examples, they don't matter - the bigger point here is that we could generate on pen and paper tens of ideas - what we are trying to solve at large fundamentally is scene representation, one of the most fundamental problems in computer graphics - and thus we can not only "interpolate" between lots existing techniques, but also we will find related techniques all over computer graphics: from level of detail to lightfields, from VR to photogrammetry, from point clouds to mesh fairing and so on.

We will need a compass, a method to explore this space.

Exploration vs exploitation, I wrote a bit about it here, this is the land where being literate helps, as well as being a "hacker" - being able to quickly prototype, extract data, from doing systematic pen-and-paper sketches to bending existing code to prove unknowns. See also "how to render it", again a recent post from my old blog.

Making this extra hard is that we don't want to optimize primarily for performance, but for quality per bit - which is one of the most complex things in computer science.

Prototyping: branch & bound.

The key to R&D is to fail fast, prototype as quickly as possible, having in mind what are the actual risks and what you pretty well know it should pan out, observe the result, rinse, and repeat.
This grind is like a human a* search, where at each step we evaluate what to try next with some heuristic - based on the researcher's experience. Ideally, the heuristic is an approximation of how far we are from our target (the optimal solution to the problem), but in practice that never is the case: even if we get the sense that certain ideas might be great we always consider the cost of exploring a given branch.
There are switching costs to trying different approaches, but also infrastructural costs. Certain things happen to be much easier to try than others, because the technology is already mostly there, or because what's needed can be coded efficiently with the tools at hand and so on.

This is true I think both for the individual practitioner, like in this case, myself working in my spare time, and for an industry at large, where the presence of certain frameworks can pivot a field creating feedback loops that are both amazing for efficiency, but can also put blinders to alternative ideas.
It's not the topic of this article, but something good to keep in mind, perhaps sometimes if we want to encourage new ideas, a way to enable that is to lower the barrier of entrance for trying out things in a given conceptual framework. Nobody wants another string theory cargo cult!

Once we decide on doing a prototype to shine a light on a given idea, we should have clear in mind what we need to prove - i.e. what are the actual risks and unknowns, and try to shortcut, if possible, to these.


Pen, paper, and your meat-based NN to hallucinate the probable results is the cheapest form of prototyping...
First thing, can we do something entirely trivial? Octahedral impostors are very fast to generate, and a known quantity, there are plenty of tools and plugins for almost any engine that we can use to try them out.
Typically they are used as LODs for artist-made objects, where the artist has some control over what gets considered an LOD unit, so the main risk for this use case would seem to be that they might not work very well on arbitrary polygon soups, where geometry might be strongly non-convex, with lots of different parallax layers.


Testing the automatic splitting of a city into a set of octahedral impostored grid cells.
This testing was done by a technical artist (thanks Chandra!) and it's kind of what one would expect - indeed octahedral impostors suffer from non-convexity, but at the same time, at a reasonable distance, they were holding up well enough. But one problem was immediately apparent - the limiting factor is image size. Octahedral impostors are quite wasteful, they require huge textures to look decent.

In hindsight, this is obvious, as they primarily resolve visibility by baking multiple viewpoints, and couple appearance with visibility. We probably want to encode a g-buffer for appearance (normals, albedo, roughness...), to be able to do relighting, so that ends up being a lot of data. That clearly cannot be the best form of encoding, bit-wise, and makes sense only for highly instanced objects!

Could we do better? Well, surely we can think of decoupling the two!

Store only depth per viewpoint, then go from there to some UV coordinates to access surface properties. We could employ some projection-based parametrization, for example, tri-planar mapping, or store some auxiliary data. Perhaps there are ways to store a UV map that would not get screwed by the octahedral interpolation? Or perhaps it's time for me to implement the Polycube map idea, which I remember thinking was cute, effectively a tri-planar mapping on steroids...

Even the visibility can be optimized, if we can pay a bit more during rendering to liberate ourselves from a fixed set of viewpoints to interpolate from, we could search for an optimal set of projection planes... And if I'm storing just depths from a set of views... then I'm sampling points on the geometry, could we render via point splatting instead? To a cached billboard impostor?


Branch!
Interesting ideas, but now we need to code a bunch of things, so before we deepen this, can we cheaply explore a bit more? Well, the other trivial idea to try is to use existing LOD systems and see how they perform. Many LOD libraries have a concept of "remeshing" LOD, where, with some unknown magic, a solid mesh is generated from an arbitrary triangle soup, with a unique UV mapping, which is then used to reproject surface attributes (normals, materials...). Simplygon offers such functionality, so does InstaLOD, and I think this is also how Unreal's HLOD works, and I hear Unity might have added an "AutoLOD" functionality along the same lines.

Turns out, this works very well. Well enough that we can confidently spawn an effort to solve the other side of this - how to automatically partition the world, how often chunks would be needed to be generated or updated - which in turn would keep a stream of information on how fast does the impostor method has to be, what features it needs to have, how much data it can generate and so on.

At the same time, existing software seems to be quite slow - for some reason - dangerously so. How hard is it to remesh a polygon soup? Can we try? Well, I think I can whip something, with a bit of help from the pandemic...
See, during the beginning of the pandemic, bored to death in my San Mateo studio apartment, I picked up jewelry making. At first, I did everything by hand, carving silver clay, but then I started to do things procedurally, to be 3d printed in silver. Of course, being an engineer (and somewhat of an ex-demo-scener even), I write all my algorithmic art in code from scratch - that's a story for another day - but tl;dr: I had to boolean hundreds of primitives together to create a printable mesh.


Now of course anyone that ever tried mesh booleans knows they fail, and that was the case for Blender as well. And of course, the solution to robust computational geometry is to work in voxels instead, so back then I already had made some blender-python scripts to union arbitrary polygon soups. Can this be turned into something that generates a low-poly mesh?

The idea is simple, in Blender, we make a script to:

1) Voxelize a scene (using Blender's OpenVDB integration)
2) Decimate the resulting mesh (using standard QEM edge collapse)
3) Create an auto-UV parametrization
4) Bake normals and other surface properties from the high-resolution scene to the new mesh.
5) Check how good and how fast the system is!

This took a couple of days, partially because I'm still a Blender beginner, partially because even if it made a lot of progress in the decades, and now is legitimately a great 3d software, partially because it still has some warts: notably, its scripting is a weird interface that mostly automates UI (think select, do something, select something else...) even if it also has some direct methods. Also, it's hard to evaluate performance because there is no way (and I even looked at the source code, and compiled the whole thing - which was surprisingly easy) to tell Blender to disable its interactive node evaluator whilst adjusting properties of said nodes programmatically.

Regardless, I quickly got this:

Left to right, top to bottom: Original, volume, remeshing, simplification.
...which looks good, even more so considering that the voxelization here is not an SDF, but an occupancy-based volume and the volume mesher thus cannot optimize vertex locations very well - thus "forcing" me to generate a high resolution voxelization to properly capture all model features.

I kind of knew this would work TBH, because even if it might look like we made the problem harder for the decimation by creating such a high poly intermediate mesh, one of the hardest parts in edge collapse is that the algorithm cannot really change the initial topology - thus here the remeshing creates, yes, a bigger mesh, but an easier one to deal with, having already merged all geometry that is near enough, eliminated buried geometry and so on.

Let's atlas the mesh and bake colors and normals, and we get something pretty convincing already:

Source scene, UV chart, baked color-normal low poly.
...in fact, the main issues here are that 1) I'm not great at matching Blender's rendering between the two models (as it uses physically based stuff and raytracing, while the impostor mesh has nonsensical normals) and 2) I could not tune the raytracing-based baker to behave exactly as I wanted.

Unfortunately, the performance of this whole thing is still not great, both because the simplification from such a high poly mesh takes some time, and because well, raytracing... Time to write some C++!

But first, branch again! While doing all this I was also toying with another idea. Can I directly generate a low-poly "wrapping" mesh that is good enough? Create a mesh that has just enough resolution to capture the major features of the scene, a sort of concave hull that then we can "shrink-wrap" to the original scene?


Directly generating a low-poly mesh, without decimation. In the bottom-right, an extreme version.
Probably! At this point, we are running close to the limit of what can be done with readymade tools. Blender's shrinkwrap does not do exactly what I want (it only moves vertices, but it cannot check that triangles themselves are near the target surface) and I would need to change its source code (Blender does not seem to provide ways to make C++ plugins) or, probably worse, work on polygons via blender-python.

What have we learned thus far? Where are we with our branching exploration?

1) Octahedral impostors are too wasteful - but likely we could optimize them, and they also hint at point clouds and heightfields to be attractive, if we can cache "transcodes".
2) Voxel-based remeshing is not hard, but either we find a good way to generate a reasonable initial mesh, or we need to spend time in the decimation.
3) Raytracing to bake surface attributes is ridiculously slow, we should think of lifting the surface properties in other ways.

Enter C(++).

Here is where I thought I should start writing my own code. I could have still tested certain ideas using other tools like MeshLab/PyMeshLab, PyCGAL or Geogram, but at a given point it starts to be diminishing returns as eventually I want to be able to control the low-level code.

So, where do we pick it up? I still don't want to open idea #1 because I feel it likely needs the "transcode"/billboard cache, and if/when I want to test that system lots of other ideas would open up.
By the way, this concept of mixing cached images with rendering reminded me of Microsoft Talisman/Fahrenheit, another of these things I vaguely knew about, but never dug to any depth. Some interesting reads, embracing tiled rendering with a cached spin, for the same reasons we do hardware tiled on mobile today - memory bandwidth!

I am pretty sure I can fix #3 by using raster methods instead of raytracing - and I know #2 via decimation will work, so I wonder if I can spend a day or two trying the direct low-poly meshing idea instead.

Easiest thing, I thought, is to prototype in 2D. Here's the idea:

1) I will generate some gnarly lines to represent my test source geometry - something with terrible topology.
2) Vxelize the lines, which hey, means just to draw them, easy!
3) From there I want to determine inside and outside. AFAIK the state of the art is using fast winding numbers, but again I don't really know how that works - so I'll instead use the idea of sweeping lines and marking for each voxel how many times it has been seen occluded from the outside or not.
4) Build an SDF around the surface and interior voxels. Compute gradients from that.
5) Build a low-poly mesh by downsampling the voxelization in coarse tiles, then making a mesh on the boundary of these (Minecraft-like)
6) Shrink the low-poly mesh to fit the SDF by following the gradients - not just moving vertices, but ensuring the whole mesh (lines) minimizes an error metric / follows the SDF gradient. In my mind this is effectively a cloth solver, perhaps I could even add some constraints to penalize bending too much, as I think it's common for simple mass-spring models.


LR-TD: test set of lines and inside-out voting (in progress), SDF and low-res voxelization, low-res mesh stepping towards the SDF gradient (in progress), final low-res mesh compared to the original set of lines.
I wrote everything in CToy and it kind of worked on first try. I spent some time thinking how to uniformly sample a square with lines for the in-out voting (well, really, a few minutes with drawbot in bed at night), it occurred to me it is a fun problem, could be an interesting interview question for certain candidates. Anyhow, obviously, people already solved it if you google, but I was happy to have found an almost correct solution to the puzzle on my own.


All of these are wrong, some more than others.
And the rest of time was spent realizing that making an SDF is not easy. See, I'm dumb, so many lessons have to be learned hands-on - I thought I could just iterate per each voxel and look at some of its neighbors, take the minimum of the distance between their distances, and call it a day. I knew this would be slow, and that jump flooding is the answer, but I'm dumb and lazy. Do you see the problem with this idea? Think about it.

Well, "obviously" if you are considering only a neighborhood then your gradient will be made only of the set of directions between the center tap and the neighbors you evaluated (that's also why as an optimization, if you want to use this stupid idea, is not to consider neighbors in the same line, these would only allow you to iterate less, but don't get you any extra precision). This doesn't work especially when far from the surface, it would cause the elements of the low-poly mesh to bunch up. In the end, because I am still lazy and this is throw-away code, I still didn't do jump flooding and instead alternated between taking the minimum distance and blurring the distance field, if I'm not near the surface.

The last issue was how to "correctly" move the low-poly mesh. This is again an interesting problem if you think about it - you can compute some displacement all along the mesh elements (lines) - and this was an idea I even initially considered implementing in Blender (I thought I could subdivide the mesh triangles to get lots of interior vertices, shrink-wrap them, then compute some sort of planar fit to compute from them the positions of the to the original low-poly vertices) - but once you have them how to "roll" the line towards the gradient is not at all trivial.
Same for how much one should try to penalize vertices "bunching up" or in other words, to preserve line length. I ended up with "heuristics" (read: hacks) for all of these that looked good enough, at least, good enough for throw-away code. FWIW, it doesn't help that with these iterative solvers (ala Jacobi, Gauss-Seidel, SOR, etc) there are many ways to do things wrong (even completely wrong) that still look reasonable or seem like errors in the tuning of the energies, not in the fundamental math - and oh boy I had bugs!

Anyway, one way or the other, I had what I came for:

- I'm still not sure this will work in 3d, but I have reasonable confidence.
- The slowest part is the in-out voting, and that will be even slower in 3D, I need to think about that more.
- This entire thing can work on CPU or GPU (compute shaders), which is good to know!

Second C++ prototype.

Again, let's recap what we want to prove at this point. There is some risk around the voxelization/occlusion/SDF problem, some bigger risk still around the meshing, and some minor (?) risk around the surface attribute transfer.
I have a few prototyping testbeds/methods I accumulated in the decades, for this I'll be using a minimalistic live-coding environment I built a few years ago to prototype SDF-based modeling ideas.

FWIW - it's based on the sokol ecosystem (but levering DX11 only), integrated with TCC ala CToy and a bunch of other tiny libraries - all setup the way I like the C(++) I write from scratch: everything live, reflected, with runtime checks, with floating point exceptions, with all warnings etc.


To be honest, I spent way too much time here sprucing up said framework, porting it to ARM-EC so it could run better on my M1 Mac/Parallels/Win11 arm setup I wanted to use while on semi-vacation in Italy, adding clang-asan, but most of all, spending an ungodly amount of time chasing a memory leak (which turned out being a problem with STL :/ and some files having different iterator debug levels) and refining my use of the windows debug heap for leak detection.
Turns out, I still don't know how to track COM leaks (e.g. ID3DBlobs) - but at a given point I had to put a stop to that rabbit hole. This is a big problem for me, if I don't impose myself certain boundaries, I risk being captured by the temptation of busy work, procrastination, and scope creep - especially for R&D when I'm not constrained by production deliverables (typically). But in this case, I told myself I was going to take it easy while working from Italy...

Back to the topic. I immediately thought I should start by generating a point cloud by rasterizing from several viewpoints around the source scene. This has lots of advantages:

1) It's fast and easy.
2) It automatically removes non-visible parts of the scene, by construction.
3) I'm pretty sure I can create a voxel grid, then average all the points falling in a given cell to control the point cloud density, and generate a pretty accurate surface distance from that.
4) It would still be desirable to close holes based on visibility - mark voxels that are often occluded - but I thought I could do that with the raster too, testing every voxel (center or some random sample) against each depth buffer and counting the number of times it's occluded by it!
5) I have been toying on paper with ideas of directly using point clouds or displaced heightfield meshes - encoding depth-maps as the geometric representation - and this would allow me to try that idea too - two birds with one stone.
6) Even if I'd be using the GPU to do all this work, in the end, it's only generating depth buffers - something that should be reasonably fast with a software raster as well, would the need occur.

I wrote a few lines of code to display the depth and normal buffer I capture from each viewpoint as a heightfield mesh - mostly for debugging, seemed a straightforward way to validate I had all the math right...


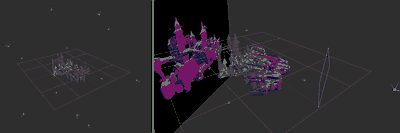Test scene surrounded by the views I'll use for sampling, and a visualization of a specific view: showing the near-far planes, a normal buffer, and a heightfield mesh reconstructed from the depth buffer and normals, with one quad per texel.
...but then I could not resist branching a second. See, the "debug" heightfield mesh looks promising enough I could be able to use it directly as my low-poly mesh. Also, I figured it wouldn't hurt to downsample the buffers and transfer them to the CPU, I would get a point cloud I could play with as well!

What I tried was to downsample the depth/normal buffers (with care, shouldn't take min or max depth here as we would like to have points exactly on the surface, not a conservative estimate - I guess plane-fitting would be possible but seems overkill for now), then create a mesh trying to optimize where the quads are split (as it's easy - why not) - and as the heuristic to avoid creating long walls along discontinuities, I figured I could simply kill a triangle if it ended up being too long.

I went with 100x100 resolution and 12 viewpoints, figured this would be small enough to compress and transmit if it works...


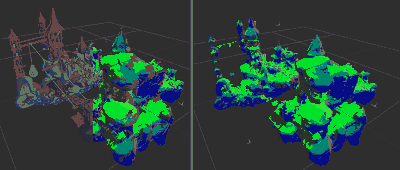Not quite good.
Turns out this doesn't work, at least, not with the naive implementation I described so far. I see three big problems:

1) Even if I try to be close to the surface, there are still triangles from different viewpoints that end up crossing each other at weird angles.
2) I have holes in the resulting mesh.
3) The surface attributes (normals in this case) are discontinuous between the views, they should be handled separately, with a global projection - but this also tells me that I wouldn't be able to simply UV map this mesh - the crossing polygons would always result in some discontinuities.

Now mind you, this is not that bad for a quick test, if I bump up the resolution I get something very reasonable, which tells me there is probably a way to tweak and encode the heightfields in such a way this works... One could use the raster again to check for triangle visibility and remove the unwanted ones that way, instead of using a length heuristic - and all of this also smells of differentiable rendering - which would be interesting to try...


But! There is also another problem I didn't mention. 100x100x2x12 means 240000 triangles, not quite that low-poly - still lower than the initial scene, but all my remeshing tests thus far were shooting for an order of magnitude less than that.

Back on track. The voxels, the SDF. Do I really need them? See, another point of view on this is that I'm just creating a virtual "scan" of my 3d scene... and there are ways to generate meshes from scans. In particular, there is this idea called "Poisson surface reconstruction" which is a pretty standard way to mesh point clouds. Should we try it?


A fuzzy point cloud (points and normals).
Again, one of the many things I only sort of know, worth spending a day looking closer. The idea is quite elegant. In layman's terms, you have a Poisson equation when you want to turn a gradient back to the field that generated it. You'll need some boundary conditions, but the math is simple.

I remember learning a long time ago that's how Photoshop's patch and spot-healing tools worked: they took a part of an image, transformed it to differentials, then solved the problem of "pasting" these differentials with a boundary set to the perimeter pixels of the destination region. Then both at Activision and Roblox we used the same equation to turn (artist-authored) normal maps into heightfields, to then bake micro-occlusion.


What do seamless cloning, normals-to-height, and surface from oriented points have in common? Poisson!
The problem is always how to solve the (discretized) system fast. Every time you have differential equations to solve on a grid, you typically end up with some iterative solver that works by inverting a matrix - just one that you never build explicitly - and to solve it fast you want to be able to have faraway elements somehow communicate, otherwise the low-frequency parts of the solution will take a long time to "diffuse" across the discretization. This typically entails some sort of multi-resolution scheme (that numerically literate people call multigrid) or some sort of frequency-space basis (Fourier, wavelets, etc).

The attractiveness of this for mesh reconstruction is that, with the right boundary conditions (Dirichlet, imposing the boundaries are outside the model), one can reconstruct an implicit function that is guaranteed to generate a closed mesh, and the method is robust to noise (which is irrelevant to us). The OG Poisson reconstruction only imposes gradient constraints, using the normals of the point cloud, but subsequently, a more precise method was invented called "screened Poisson" which penalizes the solution such that it is encouraged to interpolate the point set.

Both rely on an octree to discretize the problem, spline basis functions, and a multigrid approach - stuff way beyond my numerical analysis skills, and for which I would never write solvers from scratch. Luckily, there are many implementations of this that are open source, including one in MeshLab, so I can just plug and play.

Technically, Poisson reconstruction gives an implicit function that then has to be meshed with something like marching cubes et al. In the past, I've always used surface nets - and AFAIK the state of the art would be cubical marching squares... but we don't need to sweat it - as we get a good mesh with fewer polygons than the naive voxelization I had in the early Blender experiments, now we can decimate via edge collapse and it's extremely fast.


10k poly remeshing, visualized in MeshLab.
The resulting system works in a handful of seconds - so it's already good enough!

Conclusions?

Ok, I already wrote a lot so it's a good place to stop. I still have a lot of roads open and work to do...


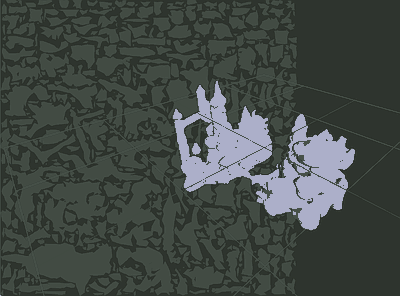Proxy low-poly mesh generated in my testbed, with its UV atlas.
I just finished my first version of the texture baking system. The idea is simple, I still use multi-view rendering (in fact right now I'm just reusing the rendered textures from the "point baking" phase):
1) For each texel, I know where that surface point would have been in world space, so I can project it to the space of a given viewpoint
2) I sample the screen-space attributes at that point (g-buffer) and also sample the depth of the surface I'm sampling.
3) I compare the sampled depth with the depth of the texel point and store the attributes in the atlas chart only if it's nearest to what is already at that texel position.


Some of the steps of the baking system, as it progresses, the texture gets more correct, and the distances stored in the z-buffer decrease.
It's pretty crude as all of this has to use point sampling, and right now I am not doing anything smart to blend multiple samples or supersample to then downscale, and even if there are reasons for this "closest" heuristic (the closest point would have the least "parallax" and thus, be "valid" from most viewpoints), it's not the best... but... to my surprise, it already sort-of works! - and of course, it's blazing fast (and super simple)!


WIP. Original vs low-poly with baked normal map. Blender doesn't seem to like my textures (or rather, I'm surely doing something wrong).
More WIP. A bit better, visualized with my own code.
I think I have something close to "shippable" in gaming parlance, but even then, it's just a first stop in the ascent to a great solution. We just proved that we can (likely) do one of the most simple ideas fast enough, and with good enough quality.

Roads still open thus far:

- The idea of direct voxelization/SDF would still be interesting. Poisson is nifty because in one go it both solves the problem of determining a surface and ensuring it's closed (inside/out classification), but for our needs, I think it would still be faster to mark voxels as in or out first, and then SDF the point cloud. Notably, it would be trivial to implement on GPU or ISPC.
- Additionally, directly generating/fitting a low-poly mesh (instead of decimating) could remove the last CPU dependency and yield a near real-time GPU meshing solution.
- Having a closed mesh is nice, but not strictly needed. There are crazier ideas to try if we allow textured planes and in general arbitrary geometry as the approximation.
- Creating a "better" octahedral-like impostor by UV-mapping attributes etc seems it still would be a great tradeoff between simplicity and potential outcomes...
- There is still the entire spectrum of solutions that would be enabled by allowing the clients to do more work, and cache it. Would be a good excuse to explore NERFs and all the other differential toys...
- If we end up needing real-time updates the impostors, and transmit deltas, we'd probably need something radically different - something with more of a fixed structure.
- Compression is TBD!


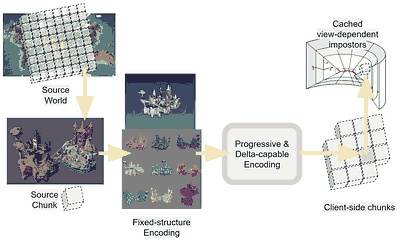Perhaps?
Addendum
Some other relevant papers. I have to admit, whilst in general, I tend to have a decent cross-disciplinary knowledge around research, lots of these were found after the fact, as once you start exploring an idea you get a sense that there should be something along these lines already out there, and with some googling and link-following, it's often possible to find things at least close enough to be interesting.
There is a limit to the usefulness of doing this - sometimes it leads to better ideas, but it can be also a time sink that results in data points that are all not quite in the right context, and thus, not answering the biggest unknowns.

That said...


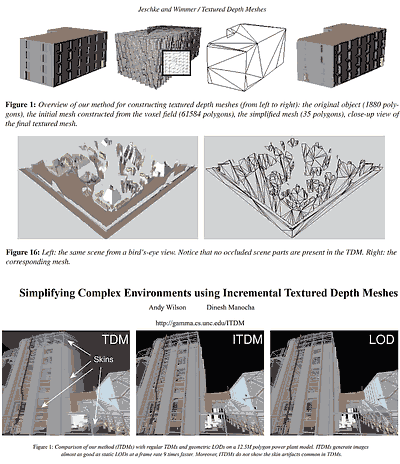Textured Depth Images by Jenschke and Wimmer, which seem to have inspired a few follow-up papers.
"Textured depth images", together with the already mentioned "depth mesh" thesis are close to what I show here. Interestingly I found that the TDM paper goes for a voxel-based remeshing (amazing!) but it ends up constructing view-dependent impostors. A subsequent paper "incremental textured depth images" seems also interesting as it builds a database of viewpoints and related approximations - in a manner very similar to what I was thinking of in my occluder tests. One day I should have a closer look.

In general, it seems that especially around the early 2000 there were quite a few ideas exploring meshes and point clouds from depth maps, possibly taken from multiple viewpoints and multiple parallax layers, for simplification and rendering.


Similar concepts, late 90ies, early 2000s.
One can connect these early ideas to later research around stereoscopic rendering (reprojection/warping), and stereoscopic encoding (RGB-D video) for 3d displays...


Lots of work around these topics - just some papers to give the idea, I don't even pretend to say these were the most influential.
...morphing then in the era of VR to lightfield acquisition/encoding/rendering ideas:


Finally, one could go from lightfields to neural encoding, to NeRFs, to differentiable rendering for optimization, and so on...